Triángulo de Pascal

"TRIÁNGULO DE PASCAL"

¿Qué es?

El Triángulo de Pascal, también conocido como Triángulo de Tartaglia, es una disposición de números con forma de triángulo, construida de tal manera que cada elemento es la suma de los dos inmediatamente superiores a él, y donde inicialmente se coloca el número 1 en los lados exteriores. 

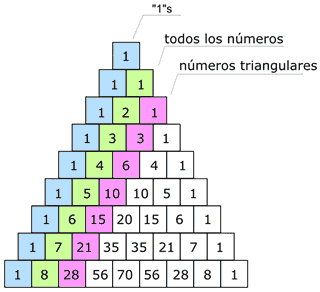
• Por ejemplo:

El triángulo de Pascal se construye de la siguiente manera: se comienza en el número «1» centrado en la parte superior; después se escriben una serie de números en las casillas situadas en sentido diagonal descendente, a ambos lados, del siguiente modo: se suman las parejas de cifras situadas horizontalmente (1 + 1), y el resultado (2) se escribe debajo de dichas casillas; el proceso continúa escribiendo en las casillas inferiores la suma de las dos cifras situadas sobre ellas (1 + 2 = 3), etc. De manera general, esto se cumple así debido a la regla de Pascal, que indica que ${\displaystyle \scriptstyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}}$ para todo entero positivo n y todo entero positivo k entre 0 y n.

Fue creado por Blaise Pascal

Relación con el binomio de Newton:

La expresión que proporciona las potencias de una suma ${\displaystyle (a+b)^{n}\;}$ se denomina binomio de Newton.

En esta expresión, lo único que se desconoce son los coeficientes de los monomios, de manera que la relación con el triángulo de Pascal es la siguiente:

Los coeficientes de la forma desarrollada de (a+b)n se encuentran en la línea «n+1» del Triángulo de Pascal.

Se puede generalizar este resultado para cualquier valor de n ∈ N por inducción matemática.

A continuación te dejo un vídeo acerca del tema.

Operaciones básicas

"Operaciones con polinomios"

Suma de polinomios

Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado. También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

Ejemplos:

1.- P(x) = 2x³ + 5x − 3

    Q(x) = 4x − 3x² + 2x³

• Ordenamos los polinomios, si no lo están.

Q(x) = 2x³ − 3x² + 4x

P(x) +  Q(x) = (2x³ + 5x − 3) + (2x³ − 3x² + 4x)

• Agrupamos los monomios del mismo grado.

P(x) +  Q(x) = 2x³ + 2x³ − 3 x² + 5x + 4x − 3

• Sumamos los monomios semejantes.

P(x) +  Q(x) = 4x³− 3x² + 9x − 3

2.-

Resta de polinomios

La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.

Ejemplos:

1.-

P(x) − Q(x) = (2x³ + 5x − 3) − (2x³ − 3x² + 4x)

P(x) −  Q(x) = 2x³ + 5x − 3 − 2x³ + 3x² − 4x

P(x) −  Q(x) = 2x³ − 2x³ + 3x² + 5x− 4x − 3

P(x) −  Q(x) = 3x² + x − 3

2.-

Multiplicación de polinomios

Ejemplos:

1.-

 P(x) = 2x² − 3    Q(x) = 2x³ − 3x² + 4x

• Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.

P(x) ·  Q(x) = (2x² − 3) · (2x³ − 3x² + 4x) =

4x⁵ − 6x⁴ + 8x³ − 6x³ + 9x² − 12x =

• Se suman los monomios del mismo grado.

= 4x⁵ − 6x⁴ + 2x³ + 9x² − 12x

• Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.

2.-

División de polinomios

Para dividir dos polinomios se procede de la manera siguiente:

• Se ordena el dividendo y el divisor  con respecto a una misma letra.
• Se divide el primer término del dividendo entre el primer término del divisor, obteniéndose así el primer término del cociente
• Se multiplica el primer término del cociente por todo el divisor y el producto así obtenido se resta del dividendo, para lo cual se le cambia de signo y se escribe cada término de su semejante.
• En el caso de que algún término de este producto no tenga ningún término semejante en el dividendo, es escribe dicho término en el lugar que le corresponda de acuerdo con la ordenación del dividendo y del divisor.
• Se divide el primer término del resto entre el primer término del divisor, obteniéndose de este modo el segundo término del cociente.
• El segundo término del cociente  se multiplica por todo el divisor y el producto así obtenido se resta del dividendo, cambiándole todos los signos.
• Se divide el primer término del segundo resto entre el primer término del divisor y se repiten las operaciones anteriores hasta obtener cero como resto.

Ejemplo:

Dividir: 

Aprendiendo TFA

"Teorema fundamental de la aritmética"

En las matemáticas, y particularmente en la teoría de números, el teorema fundamental de la aritmética, que también se conoce como teorema de factorización única, afirma que todo entero positivo mayor que 1 es un número primo o un único producto de números primos, por ejemplo: 

• No existe ninguna otra factorización de 6936 y 1200 en números primos. Como la multiplicación es conmutativa, el orden de los factores es irrelevante; por esta razón, usualmente se enuncia el teorema como factorización única salvo en el orden de los factores. 
  

Números primos: Un número primo sólo se puede dividir exactamente por sí mismo y por 1. (Debe ser un número entero positivo mayor que 1).

Números compuestos: Todo número que no es primo dentro del conjunto de números naturales, excepto el número 1. Esto se debe a que cada uno de los números compuestos debe tener uno o más divisores además de poderse dividir para sí mismo y para 1.

Establece la importancia de los números primos, ya que éstos son la base con los que se construyen los enteros positivos, en el sentido de que todo entero positivo puede construirse como producto de números primos de única manera.

Conocer la factorización en primos de un número permite encontrar todos sus divisores, primos o compuestos, una vez que se sabe la factorización en primos de dos números, se puede hallar fácilmente su máximo común divisor y mínimo común múltiplo.

El teorema fue prácticamente demostrado por primera vez por Euclides, aunque la primera demostración completa apareció en las Disquisitiones Arithmeticae de Carl Friedrich Gauss.

Euclides